大学入試を考える際に、避けて通れないのが「偏差値」です。
一般的にも認知されている偏差値ですが、「高いほどいい」という認識は浸透しているのですが、偏差値はもともとどのような決め方をしているのか、また偏差値を利用した学習計画法について詳しく知っておられる方はどれほどおられるでしょうか?
今回は大学入試で重要なデータとなる偏差値の考え方と利用法について、徹底解説をします。
※この記事は、高校数学の「数学Ⅰ」「数学B」で履修する内容をふんだんに混ぜており、数学でマウントをとる記事が続きます(笑)
数学アレルギーの方は、目次より「標準正規分布というモデル」へ飛んで、それ以降をご覧ください。
データの代表値
テストの点数など、数値として個々に存在するものを「データ」といいます。まずは、データと自分のテストの点数との関係を調べることについて解説します。
テストの点数に関して、データの特徴を表す数値を、そのデータの「代表値」と呼びますが、ここでは「平均」と「中央値」について解説します。
平均
すべてのデータの数値を合計したものを、データの個数でわったものです。
すべての数値のデータの、真ん中の数値を知るのに利用される、最も有名な計算法です。
数学の世界では、平均値を
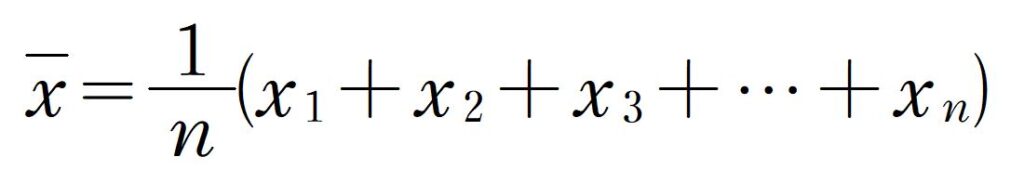
と表します。
たとえば、5人のテストの点数が42点、54点、61点、72点、86点の場合、平均点は
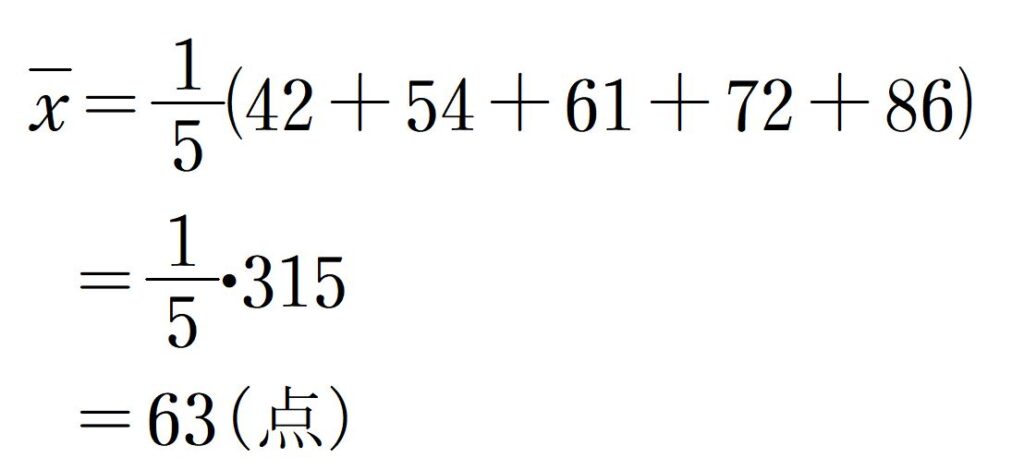
です。
中央値
データの数値を小さい順(または大きい順)に並べた時、真ん中の順番のデータを中央値といいます。
このとき、データの個数が奇数個か偶数個かによって、算出法を次のように変えます。
- 奇数個のとき
ちょうど真ん中のデータがあるので、そのデータを中央値とする。
(例)1, 2, 4, 7, 8 の中央値は、3番目のデータである4が中央値である - 偶数個のとき
ちょうど真ん中のデータがないので、真ん中に近い2つのデータの平均値を中央値とする。
(例)1, 3, 4, 6, 7, 9 の中央値は、3番目と4番目のデータ(4と6)の平均値5が中央値である
平均の罠
平均はわかりやすく、日常的にも頻繁に利用されていますが、平均には1つ大きな落とし穴があります。
たとえば今5人の人がいて、それぞれの現在の所持金が
1000円, 2000円, 3000円, 4000円, 100万円
だとします。
 みらい研修生
みらい研修生誰だよ、100万円を持ち歩いてるセレブは!



欲しい…



このブログの主、欲まみれだな!
ご覧の通り、1人を除いてはだいたい数千円をもっていると考えて差し支えなさそうですね。
ところが、ここで5人の平均を求めると次のようになります。
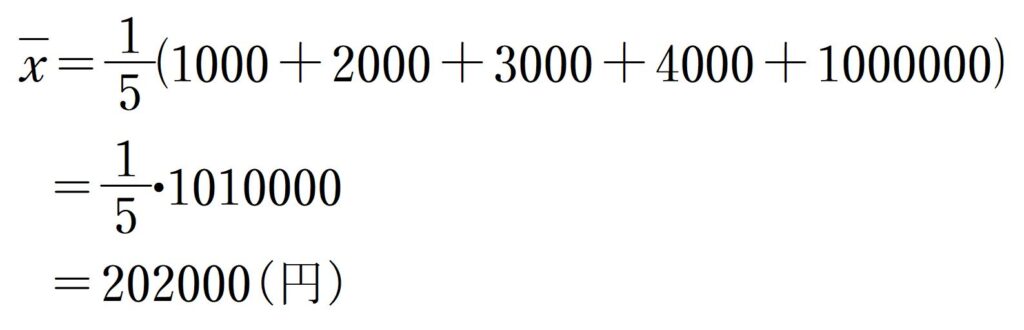
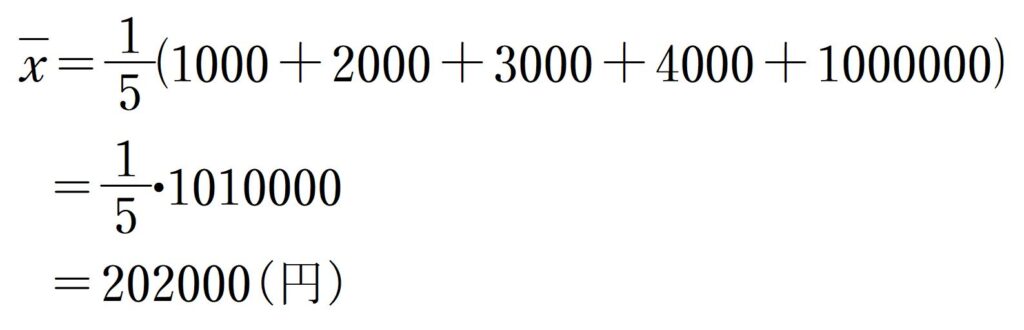
みんな20万円ほどずつ持っていることになってしまいます。
このように、他とははるかに大きな値(あるいは小さな値)が1つでも含まれていれば、平均値はその値に引っ張られる傾向があります。このような極端な値のことを「外れ値」といいます。
では、中央値ではどうなるでしょうか?
5人いるので、3番目に小さい(あるいは大きい)データとなるので、3000円となります。
こちらの方が実態に近いですね。

これに近い話として、日本の世帯ごとの貯蓄額があります。
2024年2月のYahoo!ニュースの記事からです(抜粋)。
金融広報中央委員会が2024年2月に公表した「家計の金融行動に関する世論調査(令和5年)」によると、二人以上世帯の平均貯蓄額は前年より16万円アップしたとのことです。
最新「二人以上世帯」の貯蓄割合一覧
金融広報中央委員会の「家計の金融行動に関する世論調査(令和5年)」を基に、最新データである2023年の貯蓄状況を見てみましょう。・金融資産非保有:24.7%
Yahoo!ニュース 「【貯蓄の一覧表】日本の平均貯蓄額は前年より16万円アップ。一覧表で二人以上世帯の調査結果を確認」2/19(月) 14:32配信
・100万円未満:8.6%
・100~200万円未満:6.8%
・200~300万円未満:4.9%
・300~400万円未満:4.5%
・400~500万円未満:3.2%
・500~700万円未満:6.5%
・700~1000万円未満:5.7%
・1000~1500万円未満:7.9%
・1500~2000万円未満:4.4%
・2000~3000万円未満:6.2%
・3000万円以上:12.7%
平均値:1307万円
中央値:330万円
2023年の平均値を見ると、前年に比べてやや増加していることがわかります。しかし、2021年のピーク時に比べると低水準であり、より実態に近い中央値は前年に比べて70万円減少しています。
ここで、ニュースが実際に伝えていることはおわかりでしょう。次のことがいえそうです。
- 平均値と中央値が大きく乖離しています。おそらく日本人皆が1300万円も家にあるとは思っていないでしょう。実態に近いのは、あくまでも中央値です。
- 「2021年のデータと比較したら、平均値は上がっているが、中央値は大きく下がっている」という結果は、少数の富裕層がさらに資産を伸ばしたことで、あくまでも平均が上昇したのであって、一般庶民はそれ以上に資産を削ってしまっているということです。
- 記事のタイトルでは「平均貯蓄額がアップした」と言っているあたり、実際はほとんど多くの人が貧しくなっていることを隠す意図が見えなくもな…(自主規制)
ニュースを見るときは、このような統計学上の裏を読めなければなりません。

テストの点数や平均点にとらわれすぎない
数学的な話が長くなりましたが、よくありがちなテストの点数や平均点にまつわるデータの見方について紹介します。
①点数では同じ科目どうしでも…
(例)国語と数学のテストで、どちらも60点をとった
全員で5人がテストを受けたが、他の4人は以下の点数だった
国語 50, 70, 80, 90
数学 30, 40, 50, 70
この場合、それぞれの教科の平均点を計算すると、国語は70点、数学は50点です。
どちらも60点をとったのですが、国語は平均点以下なのに、数学は平均点以上でした。
点数が何点だったかだけを見ても、全体の集団の中で取れていた点数だったかということは見えてきません。
②点数が落ちてる!
(例)1学期の数学の得点 70点
2学期の数学の点数 50点
よくありますね。2学期になって成績が落ちたと。
勉強しなくなったせいか?それとも部活動に熱心になりすぎたせいか?
とにかく「けしからん!」となるわけです。
「2学期になって点数落ちてるじゃない!勉強が足りないんじゃない?それで大学目指すの?」
なんて、嫌味の一言でも出そうな勢いです。
ところが、次の情報を入れるとどうなるでしょうか?
1学期の数学のクラス平均点 80点
2学期の数学のクラス平均点 40点
クラス平均点も落ちているのです。
なんなら、1学期の点数はクラス平均よりも悪かったのですが、2学期の点数はクラス平均以上です。



これって怒るどころか、逆に褒めた方が良かったパターンなのでは?



そういうことだよ
だから、ヘタすれば…
ボク ガンバッタノニ ミトメテ モラエナカッタ
と思って、心を閉ざすお子さまも少なからずいるかもしれません。
もちろん、志望校いかんによっては、「50点はちょっと…」とはなりますが…。
ただ、このような家庭って多いのかもしれません。
無理もないです。成績表が来れば、何といっても点数が気になりますから。
それに、平均点がどうであろうと、理解まで及ばなかった部分が前よりも多いというのは事実です。
けれども、この子はひょっとしたら1学期で平均いかなかったから、悔しくて親御さんの見えないところで努力したり、前向きに取り組んでいたのかもしれません。
このように、点数ばかりにとらわれると、お子さまの実際の取り組みや思いを見落としてしまうこともあるので、要注意です。その対応を誤って、お子さまの学習への意欲がなくなってしまうことだけは避けたいものです。

③平均点は同じでも…
(例)5人の生徒が国語と数学のテストを受けました。点数は以下のとおりです。
国語 50, 55, 60, 65, 70
数学 20, 50, 65, 80, 85
さて、ここでまず確認しておきたいことは、国語と数学の平均点は、どちらも60点と同じだったということです。
この2つのテストの違いはどこにあるかというと、それは「得点のばらつき加減」です。
見た感じ、国語の点数は5人ともお互いに近い点数ですが、数学の方は点差が激しいです。(事実、そのような現象は起こりやすいです)
そして、この違いは、今後の勉強にどう影響するのかといえば、それは順位です。
今回はわかりやすく5人だけのテストという体で説明していますが、実際は何千人、何万人(共通テストは50万人以上)という人数によるテストがほとんどですので、そのイメージをもっていただきたいのですが、
ばらつきが少ないテストは、似たような点数を取った人が大勢います。ですから、その後、ちょっとした努力でも順位を上げやすいことを意味しています。それはとくに平均点に近い人に起こりやすい現象です。また逆にいえば、ライバルが自分の近くに大勢いることも同時にいえるわけで、ちょっとした手抜きで、次の試験で順位を落としやすいことも注意が必要でしょう。
また、ばらつきが大きいテストは、順位を上げることがより難しくなります。ですから、そのようなテストの教科は実を結ぶのに時間がかかりますから、継続的な学習をする必要があります。

データのばらつき具合を表す「分散」
さて、今点数のばらつきの話がありましたので、次にそれを数値化した「分散」についての解説をします。
分散とは
分散とは、「各データが平均値からどれだけ離れているか」という考えが基本です。
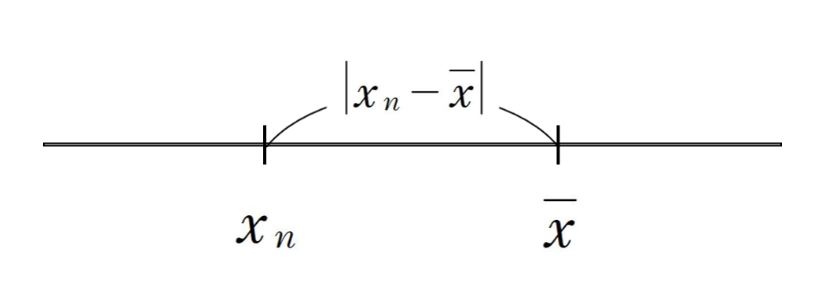

データが平均値からどれだけ離れているかは「差」で表され、それは
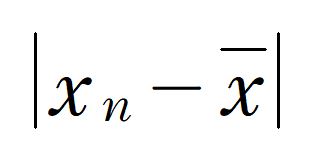
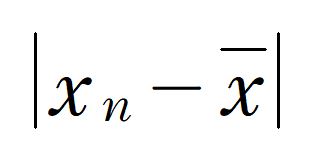
で表されます。



あれ?何この2本の縦棒?



これは「絶対値」といって、プラスの数はそのまま、マイナスの数はプラスに変えてしまう計算をするものだよ



プラスの数で考えるための記号だね



3と5の差は3-5で「―2」なんて言わないよね。マイナスは取って、普通は差を2だというね。
ちなみにこれは絶対値の性質上、
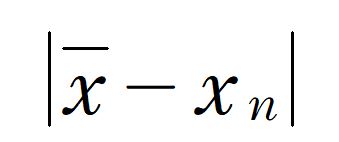
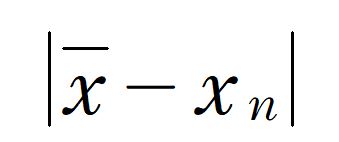
とひき算を逆にしても意味は失いません。
みんなアレルギーを起こしかねない絶対値記号ですが…。
絶対値記号がついているのは、単純に
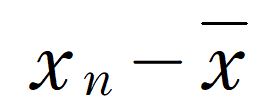
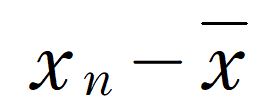
を考えると、データが平均値よりも小さければ、「差」を考えるはずの値が負となってしまうから問題だからなのです。
しかも、どのようなデータ群の場合でも、この計算を全てのデータで行って計算をすれば、その総和は0になってしまうのです。
どんなデータ群も結果が同じなら、計算する意味はないですよね。



たとえば2, 4, 9の3つのデータの場合、平均は5。
「データの値ー平均の値」はそれぞれ
-3, -1, 4
で、これらを合計したら0になるね。
だから差が負となり、数値を打ち消し合わないよう絶対値をつけるのですが、それはそれで計算がしづらくなります。
絶対値が大好きという人、病院へ行ってください!
それを解決するため、これを2乗した値にして、絶対値をなくします。この数値は実質「差」を2乗した値です。ちなみに、絶対値の2乗については、
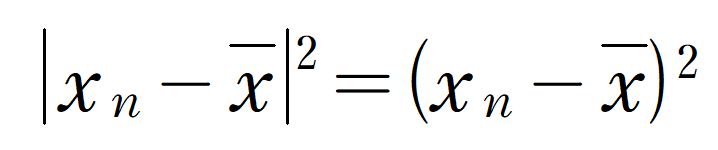
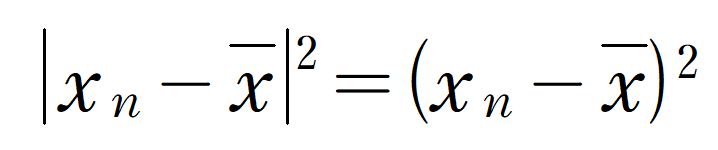
と計算されます。



上の式の| |や( )の中が-3の場合で考えると、
【左辺】|-3|=3だから、|-3|の2乗は3の2乗で9、
【右辺】-3の2乗も9だから
左辺=右辺となって、
上の式が正しいことがいえるんだ
そして、すべてのデータについて、この計算を行い、それらの平均値を計算したものを分散といいます。これを通常Vまたは![]()
![]()
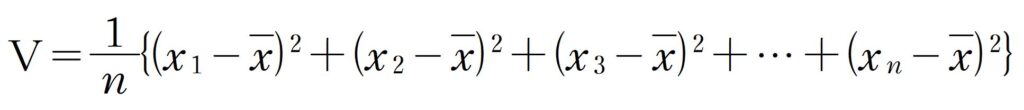
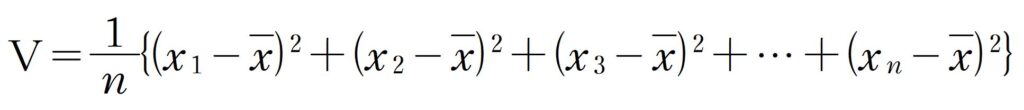



つまり、データ1つあたりの、「平均値との差の2乗の値」の平均を求めた値のことだね

標準偏差
そして、差の2乗の計算をしたので、差の値を模擬的にとらえる意味で、そのルートの値をとったものを考えたものが、「標準偏差」といい、s で表します。
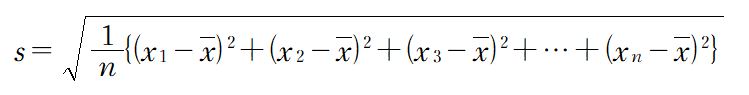
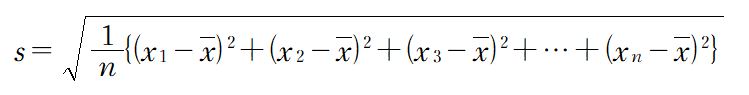
分散・標準偏差の実例
では、わかりやすく、先ほどの③の国語と数学のテストの例を用いて、平均点がどちらも60点のテストどうしでしたが、分散がいくらになるのかを計算してみましょう。
(例)5人の生徒が国語と数学のテストを受けました。点数は以下のとおりです。
国語 50, 55, 60, 65, 70
数学 20, 50, 65, 80, 85
それぞれの分散は、次のようになります。
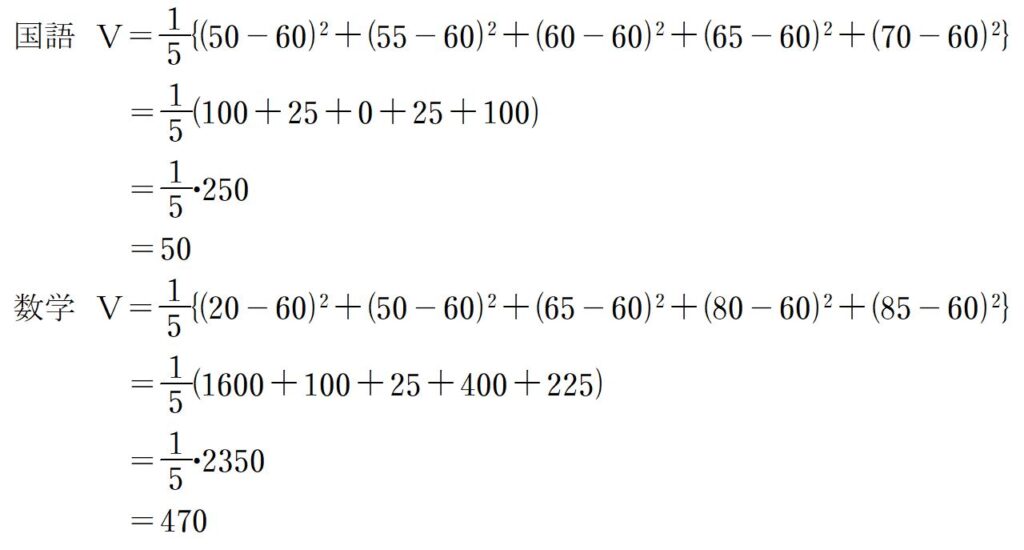
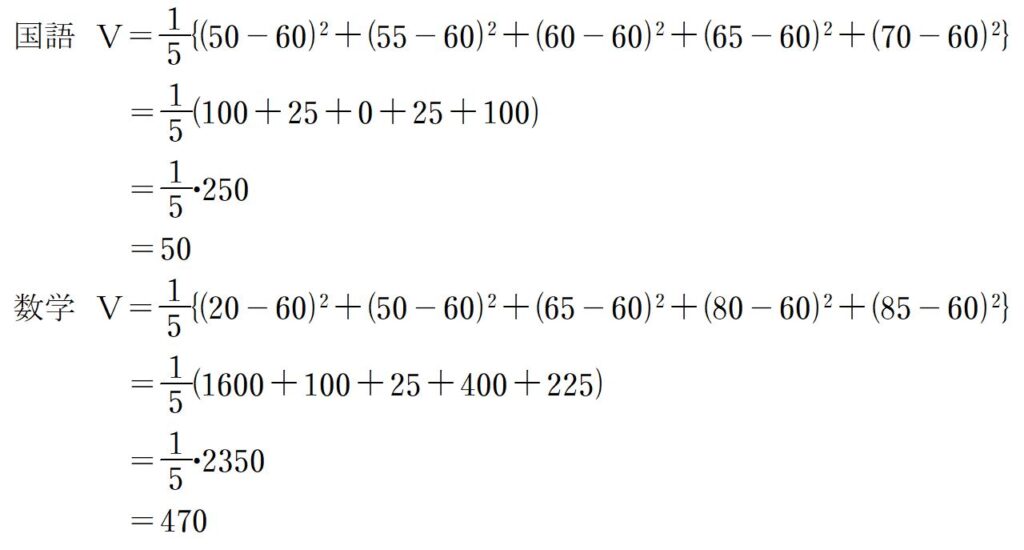
分散の値は「?」という感じですが、数学の方が国語よりも点数にばらつきがあるということは何となくわかります。
ちなみに標準偏差は、
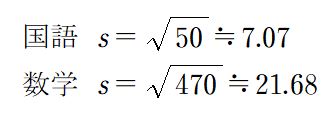
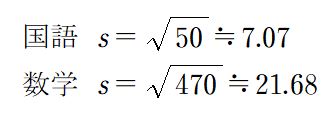
となり、国語は7点、数学は21点ほど、平均的に1つのデータあたり、平均点と離れているということがわかります。
それぞれのテストで異なる分布
平均点や分散の値で、そのテストの受験者の達成度や、得点の散らばり具合がわかるという話でしたが、ただそれでは試験が異なれば、違う分布を表すこととなり、成績の比較ができなくなります。
次の課題として、そのように試験が変わっても同じように考えられる指標が欲しいということになります。
それは、異なる分布を変換させて、共通の分布のデータに変えれば、成績の比較が可能になるのではないか
ということになります。
その理想となるモデルが、標準正規分布となります。

標準正規分布というモデル
標準正規分布の前に、正規分布について触れておきます。
正規分布とは
ここは数学を極めるための場所ではないので、厳密な定義は省略しましょう。



いや、十分数学出てきてるし!



シー――ッ!
簡単にいうと、正規分布とは、平均値と中央値(真ん中の順位の人の点数)と最頻値(人数が最も多い点数)が等しい値で、分布が左右対称になっているものととらえてくださって良いでしょう。
横軸を得点、縦軸を人数としたときの、大まかなグラフはこうなります。
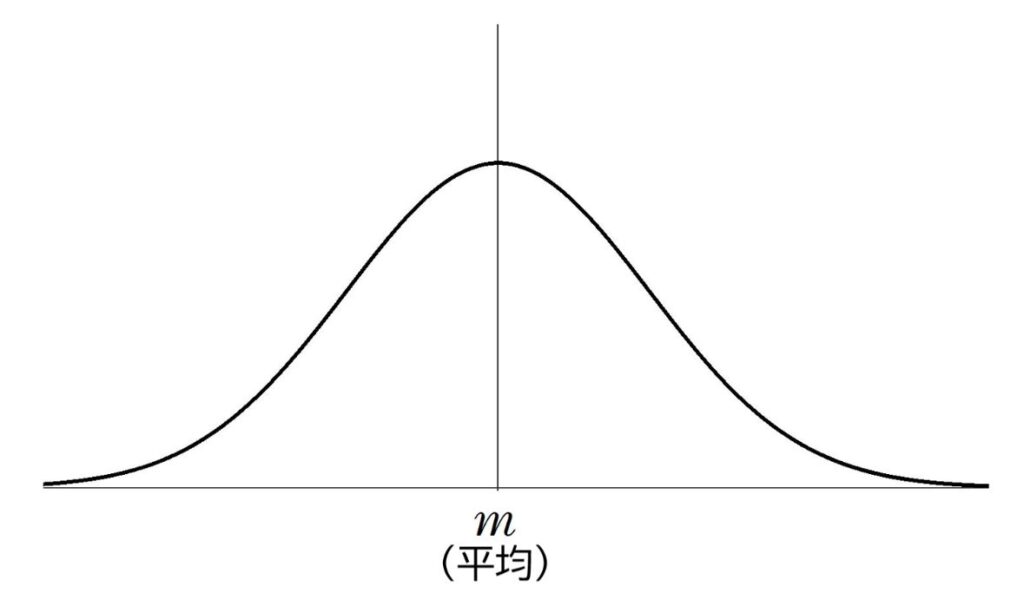

たとえば人の身長の分布などが該当します。
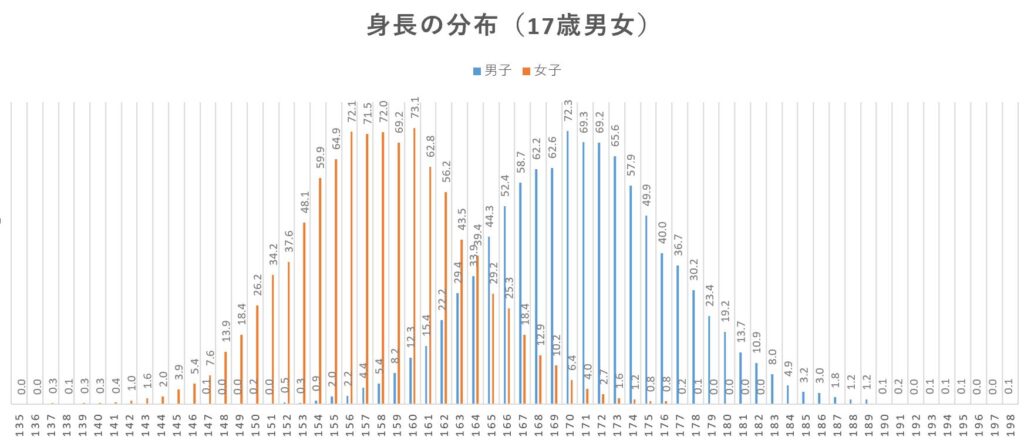

横軸:身長 縦軸:人数割合(‰)
(出典:政府統計の総合窓口 統計でみる日本『身長の年齢別分布』よりブログ主作成)
もちろん、模擬試験や共通テストなどの成績の分布も、このような正規分布にしたがうかたちをとります。
標準正規分布
さて、多くの人数が受ける試験で、テストの点数をX点、平均点がm点、標準偏差がσ(「シグマ」と読むギリシア文字です。Σの小文字ですね)であるとします。
このとき、得点の分布は正規分布にしたがうことが知られています。
この状態を
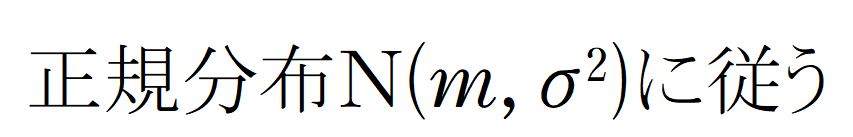
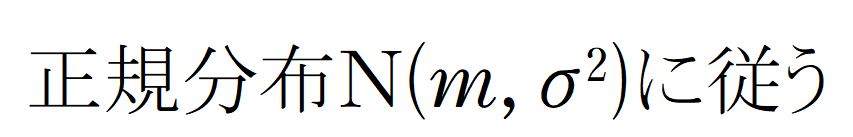
といいます。



N( )の中は、「平均,分散」あるいは「平均,標準偏差の2乗」って書くってことだね
一般には、次のことが知られています。


正規分布N(0, 1)に従う分布のことを標準正規分布といいます。
標準正規分布の特徴
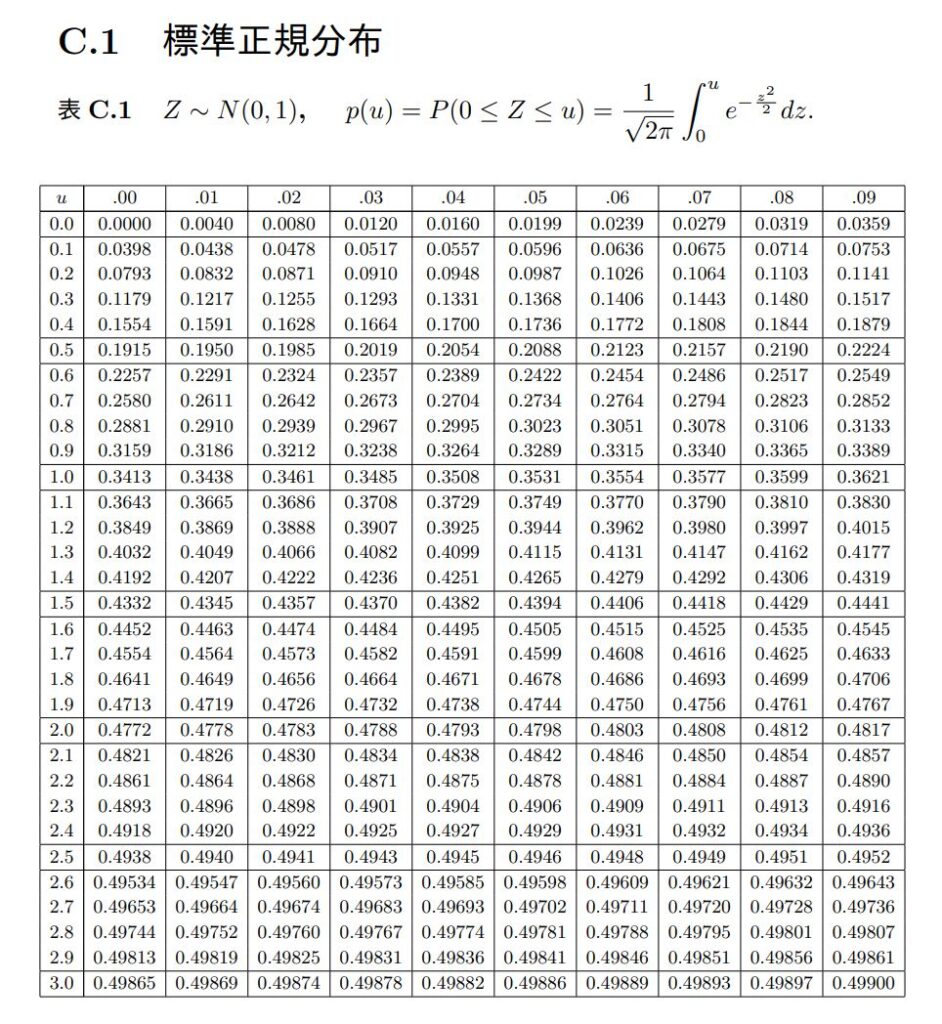
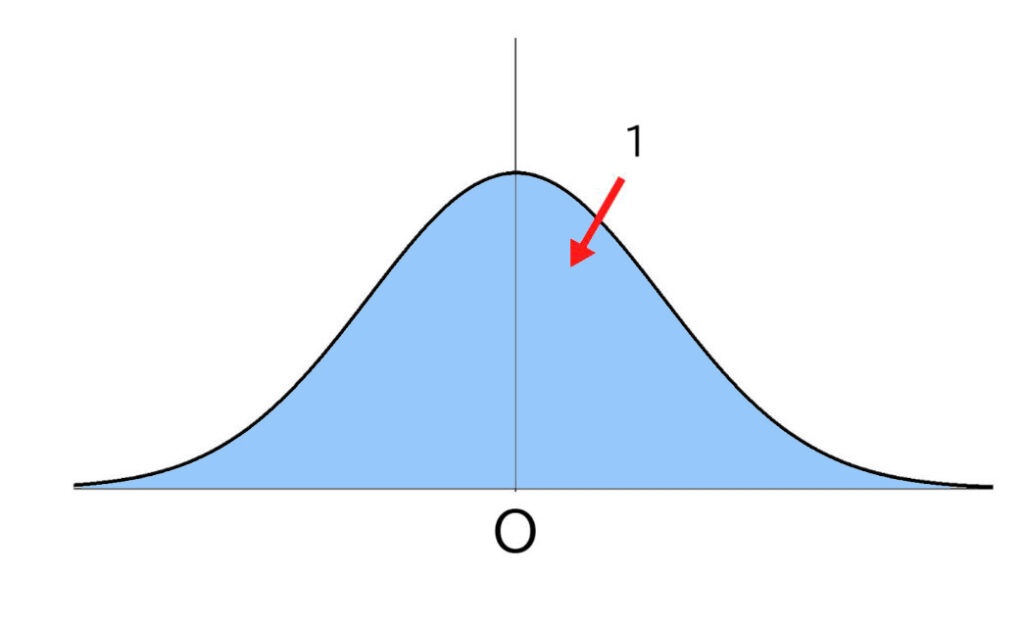
Zが正規分布N(0, 1)に従うとき、0≦Z≦u となるデータが、全体のデータを1としたとき、どれくらいあるのかを計算できます。それは「標準正規分布表」を利用することで知られます。

(出典:『標準正規分布』)
これは、標準正規分布の曲線の中央がZ=0であることをまずおさえておいてください。
ちなみにこのラインは何を意味していたでしょう?
そうです、平均点を取った人の層でしたね。
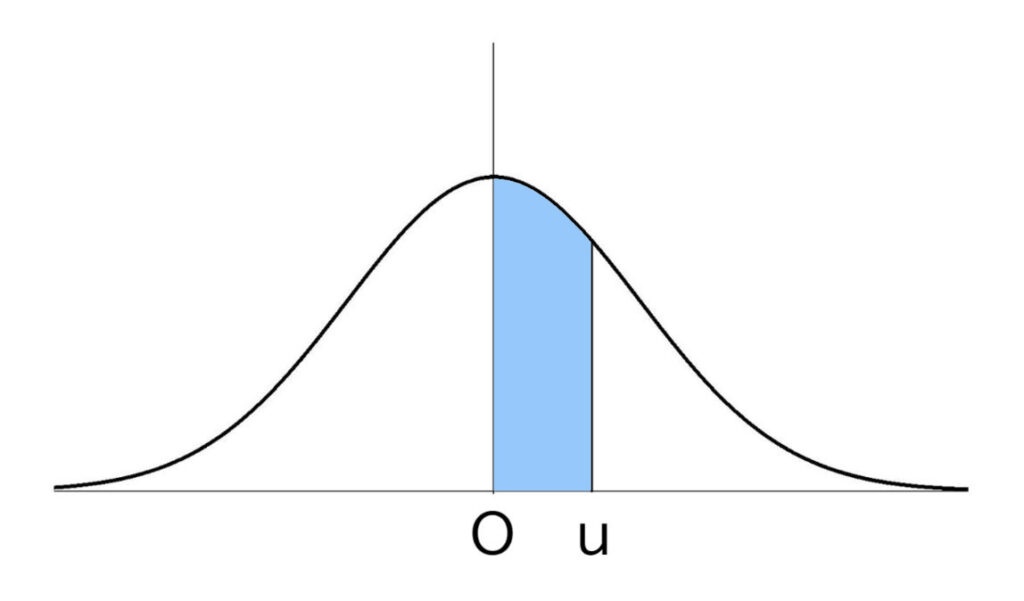

このとき、上の図の青い部分の面積が、横軸と曲線の間の部分の面積を1としたときの値となります。
言い遅れましたが、この標準正規分布を表す曲線の式は
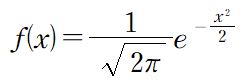
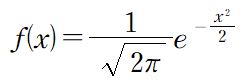
であり、
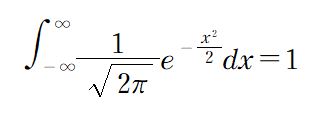
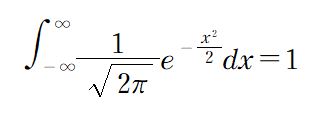
が成り立ちます。

たとえば、u=1.43としたとき、標準正規分布表から1.43に対応する数値を読み取ります。
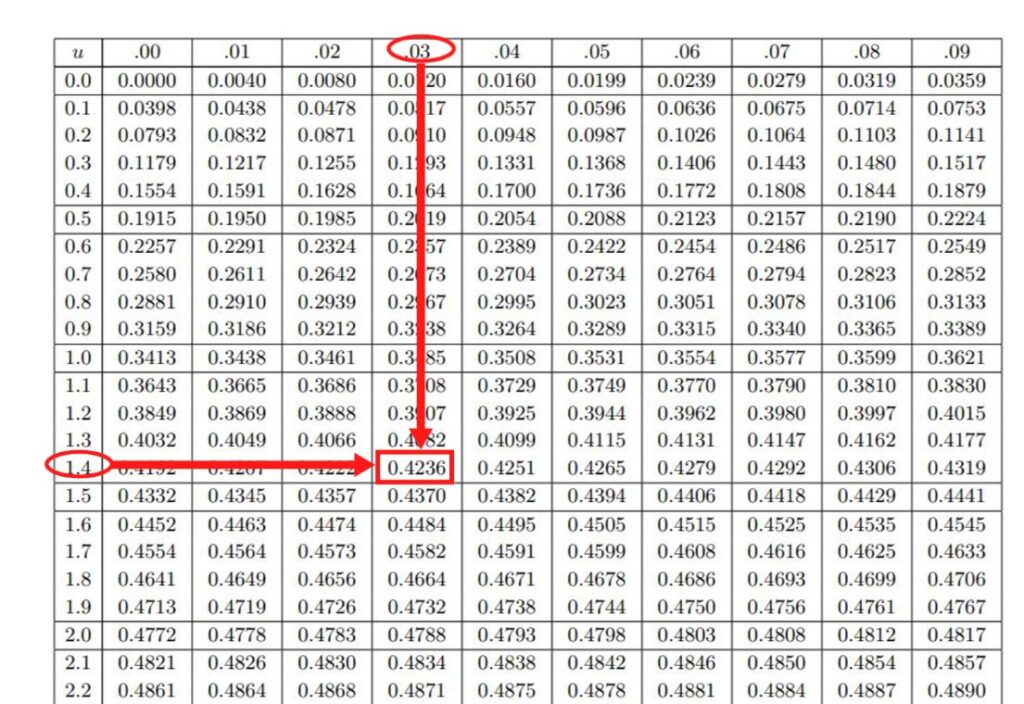

uの値の小数第1位までの数値を横軸に、小数第2位を縦軸に見て、ぶつかった数字を読み取ります。
u=1.43の場合、「1.4」と「0.03」が交わったところの数字が「0.4236」とあります。
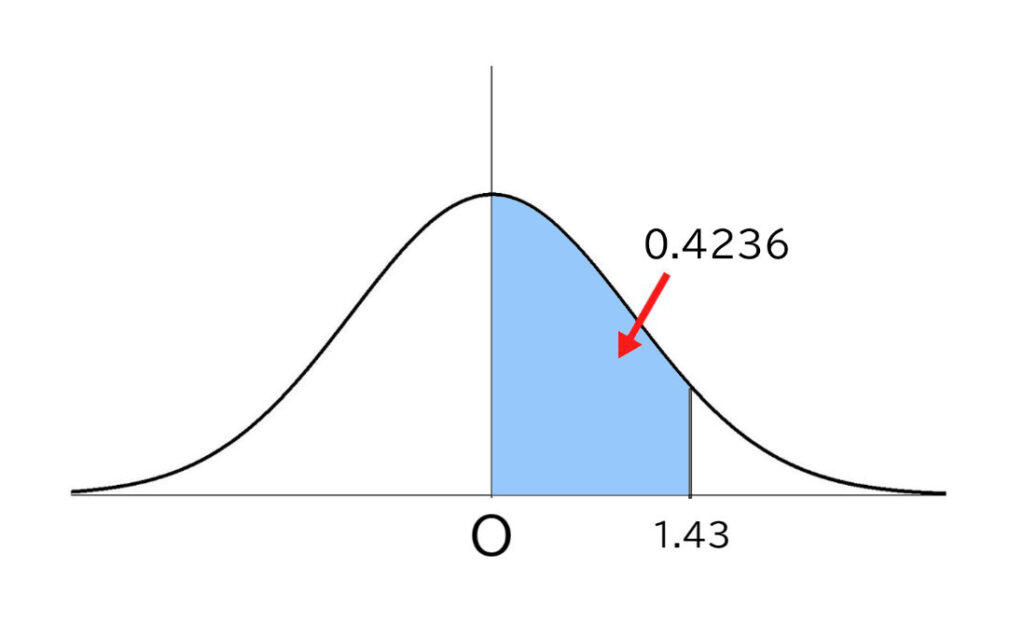

この「0.4236」は何を意味しているのか?
それは、真ん中のラインからu=1.43とされる場所までに入っているデータ(つまり人数)が、全体の42.36%いるということがわかるのです。
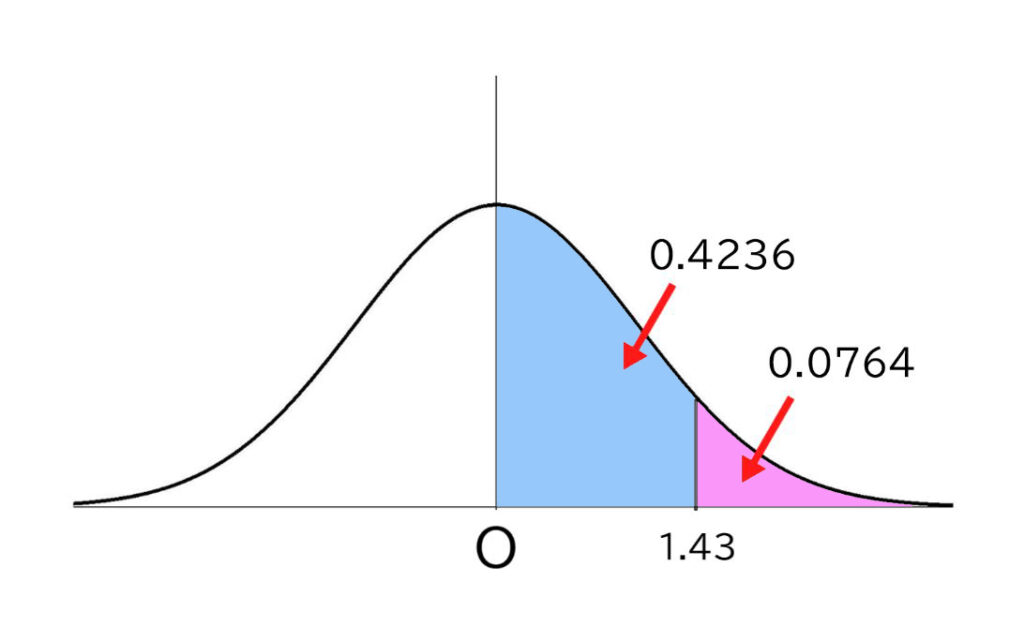

もう少し言いましょう。逆をいえば、右端(1.43よりも右側)の層のデータ(人数)は、全体の7.64%となります(Oから右全体が1の半分の0.5だから)。
そうです、この層の人は上位8%内にいるということがいえるのです。
…と言ったら、ピンときた方はおられますか?
これは、試験の偏差値と関連させれば、「この幅の偏差値の層には何人いる」とか、「自分は目標とする大学に合格できる力をもつまでに、あと何人追い越せばよい」などといった計算ができるということです。
その実用例は後ほど。
標準正規分布の試験への活用法
それでは、実例を交えて、標準正規分布を利用した成績の活用法について解説します。
たとえば、ある数学の試験で次の結果であったとします。
数学の試験の結果
- 受験者数1000人
- 平均点55点
- 標準偏差12
- 得点が正規分布に従っているとする
まずは、標準正規分布に変換をします。
例の変換式を使うと、次のことがいえます。


たとえば、この試験で、お子さまの試験の点数が64点であったとします。
このとき、次のようなことが調べられます。
上位何%にいる?
お子さまの点数が64点ですので、X=64としてZを求めます。
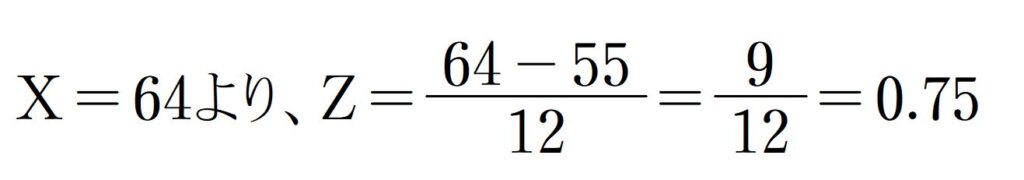
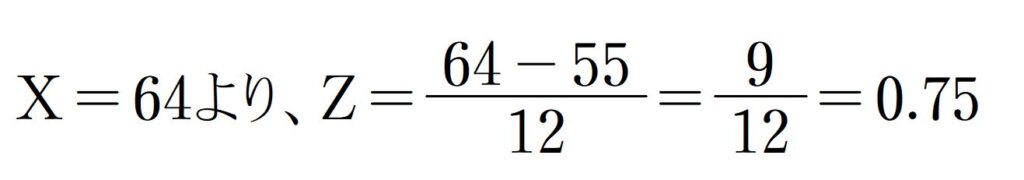
標準正規分布内で、Z=0.75の場合の割合の値を、数表から割り出します。
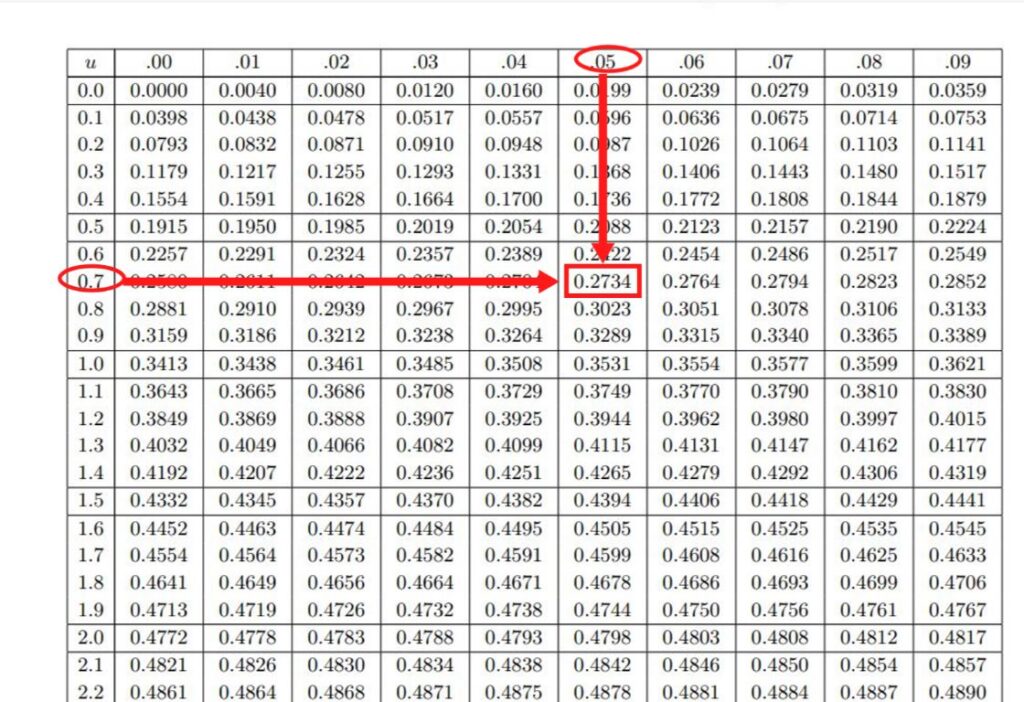

数表で求めた「0.2734」、つまり「27.34%」とは、平均点からお子さまの点数までの間の成績の受験生の人数が、全体の27.34%いるということを表します。
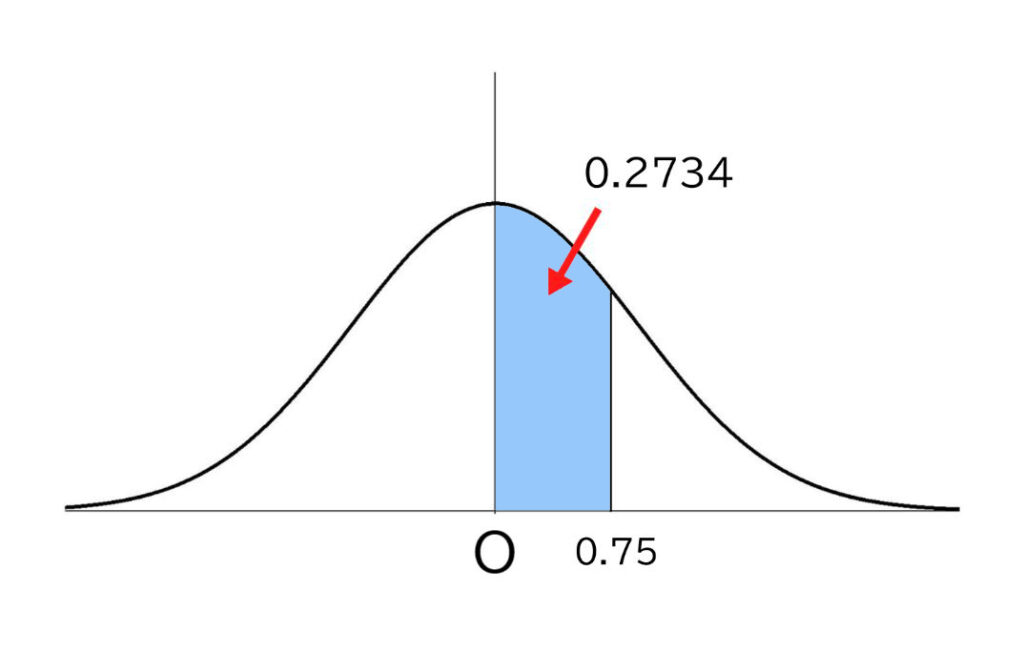

そうすると、そこよりも上位の部分の割合は、分布の右半分の50%から27.34%を引いた22.66%となるので、お子さまは上位22.6%の層にいることがわかるのです。
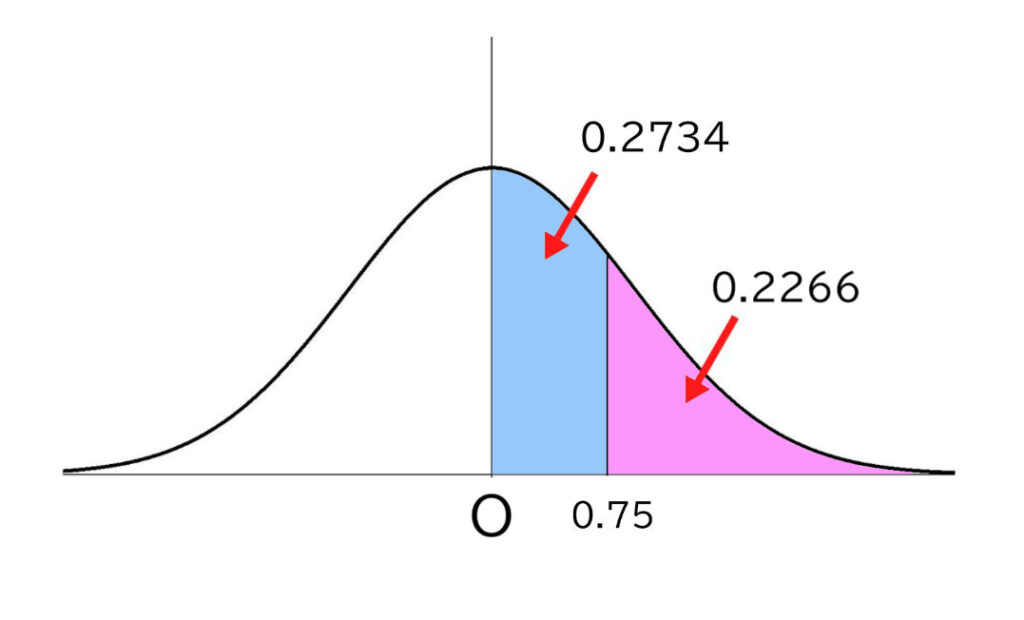

普通は全体順位は成績表に掲載されているはずですので、全体で何位かということは、調べなくてもわかるのが普通ですが、上位22.6%ということは、受験者数が1000人ということであれば、1000×0.226=226(位)ということで、これが計算上の順位として求められます。同点の受験生もいたり、変換式を用いたりするので、多少数値は変わるかもしれませんが。
あと◯点多く取れれば、順位はどれくらい上がる?
「このテスト、75点取れていればどうだったんだろう?」という疑問をお子さまがお持ちだったとします。あるいはやりようによっては、その点数まで行けたかもしれないということであれば、お子さまの点数が75点と仮定をして同じように分布の性質を用いて計算してみましょう。
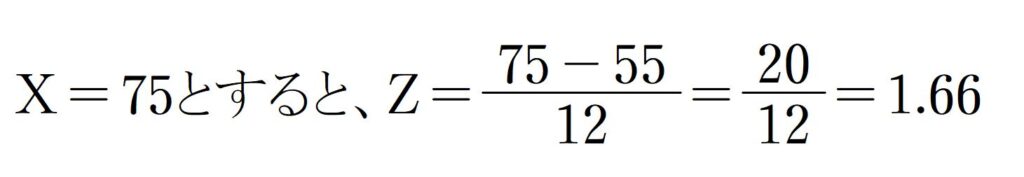
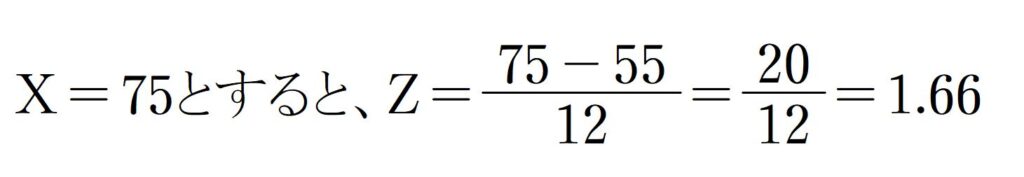
Z=1.66として、標準正規分布表で数値を拾います。
そうすると、0.4515と出ます。
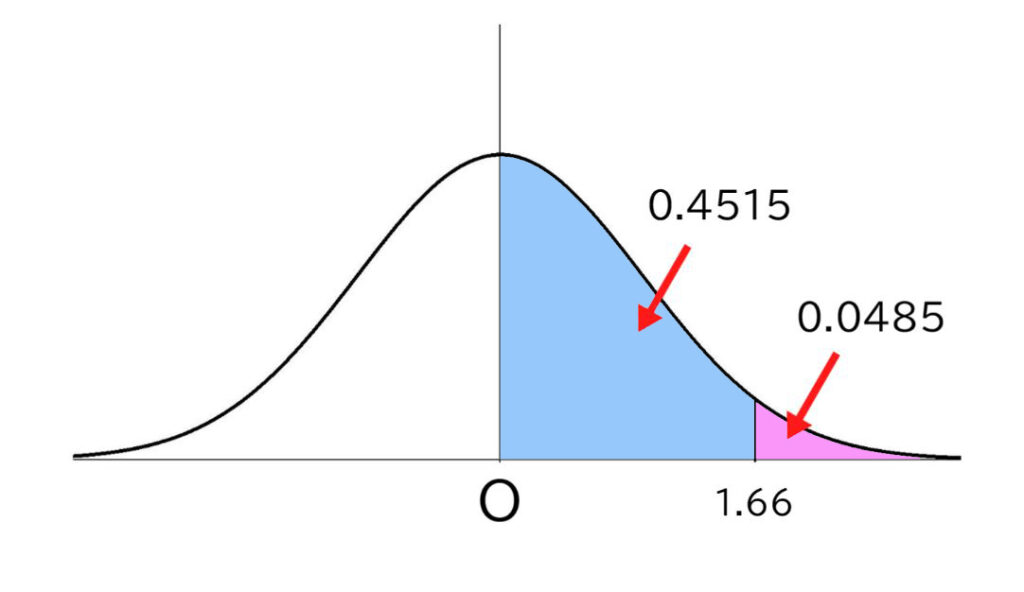

そして、上位層は50%から引くので、4.8%とわかり、もし75点を取っていれば、上位4.8%、つまり48位にまで上がることがわかります。
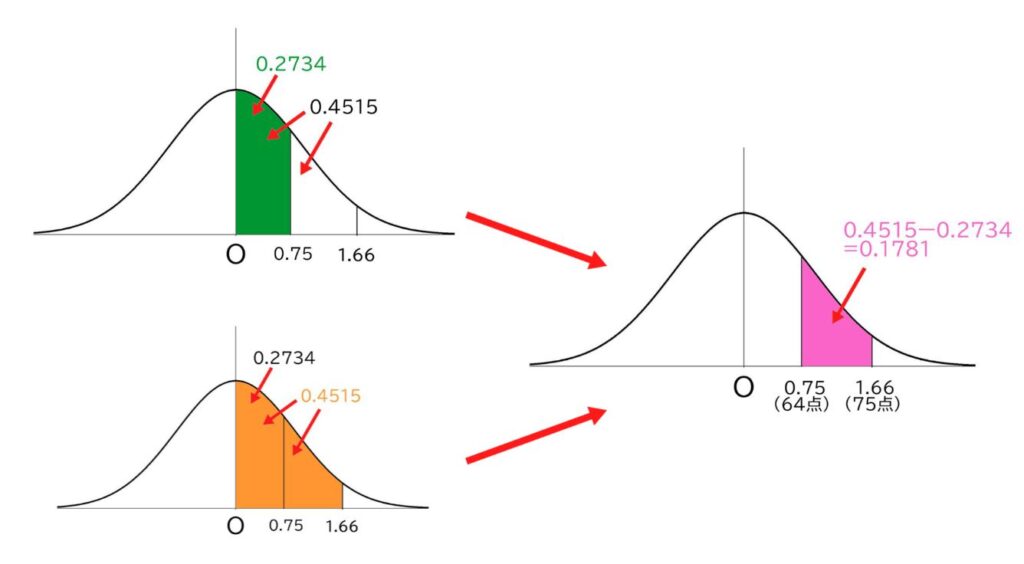

また、「64点だったのが75点になると、何人抜けるのか?」という疑問も起こるでしょう。その場合は、2つの割合をひき算することによって、2つの間の層の人数の割合が調べられます。
この場合では、17.8%の人数を抜けることがわかり、人数としては、1000×0.178=178人を抜けることが調べられます。
平均より低い得点層は、左右対称性を利用する
それでは、平均点よりも低い点数の場合の計算法について紹介します。
たとえば43点を取った人の場合で説明します。



みんな大好きZの計算からだよね。もう慣れてきたぞ



お、その通り。察しがいいね。
何だよ、みんな大好きって(笑)
話を続けましょう。
まずは43点の場合のZの値を調べます。
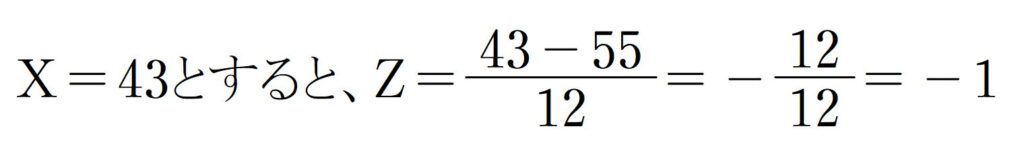
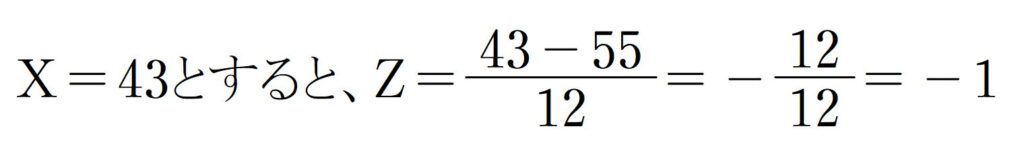
Z=ー1のときの割合の数値ですが…。
そうです、数表にはマイナスの値は載っていません。
それはなくてもいいからです。
標準正規分布の場合、左右対称の分布なので、Z=ー1のときの割合(-1≦Z≦0)は、Z=1のときの割合(0≦Z≦1)と等しく、表ではZ=1で読み取れば良いのです。
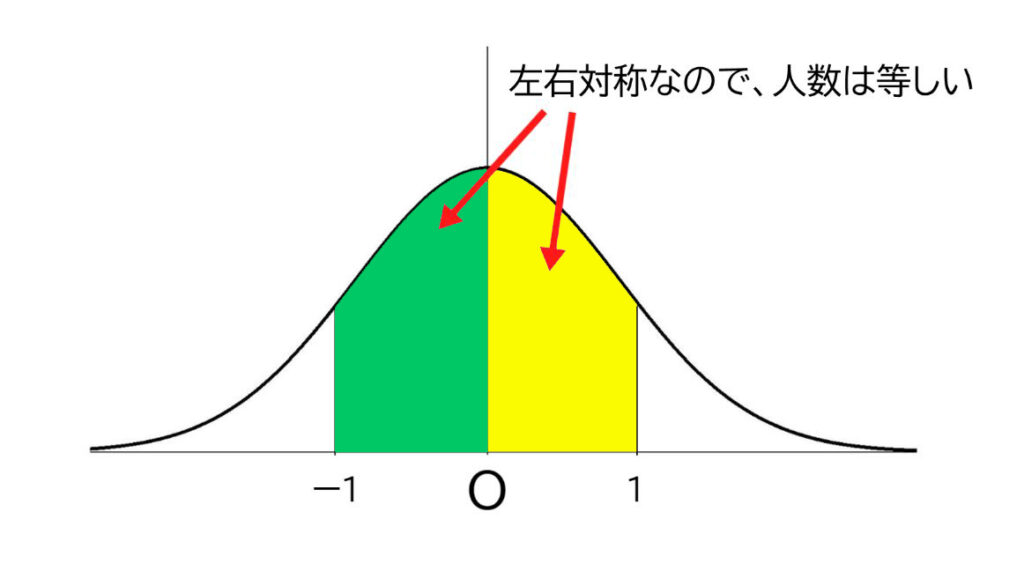

表の1.00のところを見たら0.3413となっていますね。
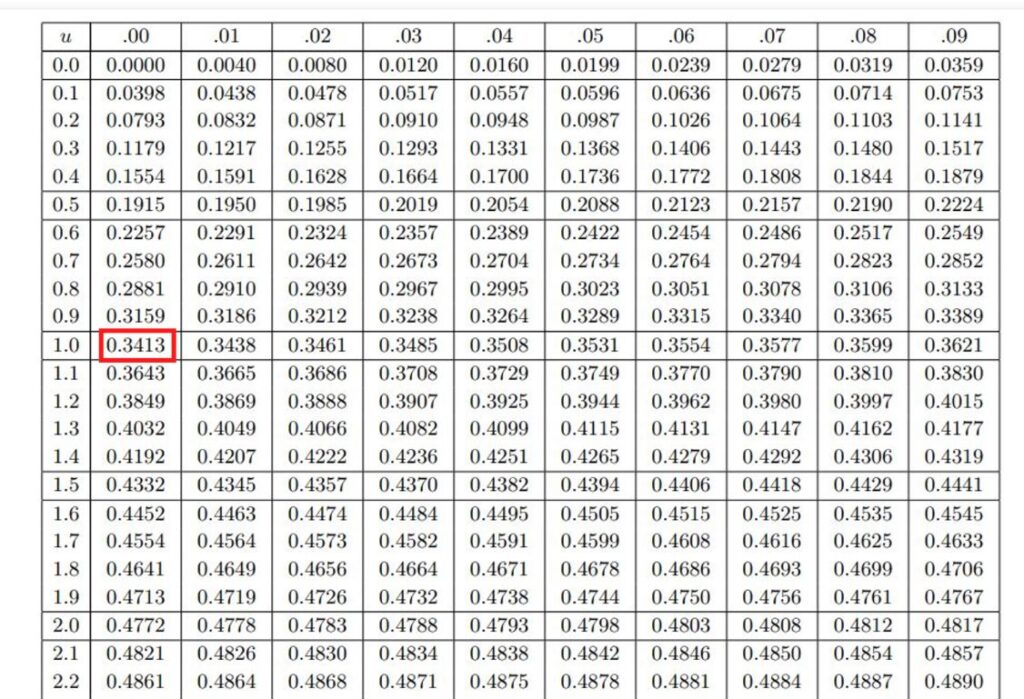

したがって、右半分の0.5を加えて0.8413とすると、上から数えて84.1%のところの位置だということになります。つまり1000人中841位ということです。

標準正規分布から偏差値を考える
試験で利用される「偏差値」は、この標準正規分布の考えによるものです。
お待たせいたしました。
それではみんな大好き偏差値の説明をいたします。



前置き長すぎるよ!



たしかに。でもここまで細かく書かれているブログって、あまりないかもしれないな(網羅性)



カクノキツイ…
標準正規分布化させて作る偏差値
正規分布に従うデータ群において、
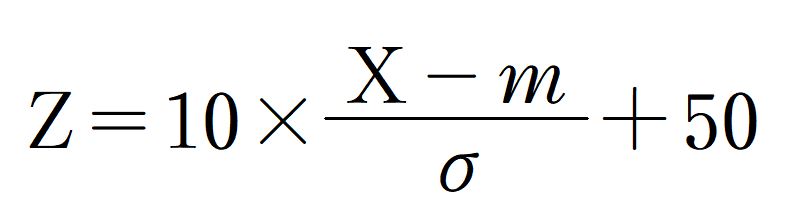
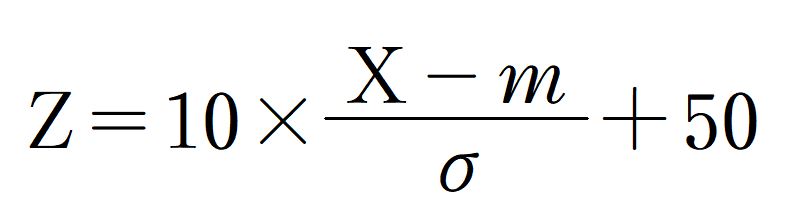
と計算されるZを実は「偏差値」と呼びます。



ところで平均点を取った人の偏差値はいくらになるか知ってるか?



えーと…、いくらでしたっけ?
はい、これ重要ですね。平均点を取った人は、上の計算式でX=mという状態ですね。
だから(10×分数)の部分が0になって消えるので、Z=50となります。
平均点を取った人の偏差値は50です。
その他、あまりにも点数が低すぎると、偏差値が出ないのではないかという都市伝説があるのですが、たとえ試験が0点だったとしても、普通は何らかの偏差値は出てきます。まあ…、低いですが。
偏差値の計算
平均点が60点、標準偏差が15である試験で、お子さまが69点を取ったとします。この時の偏差値は、
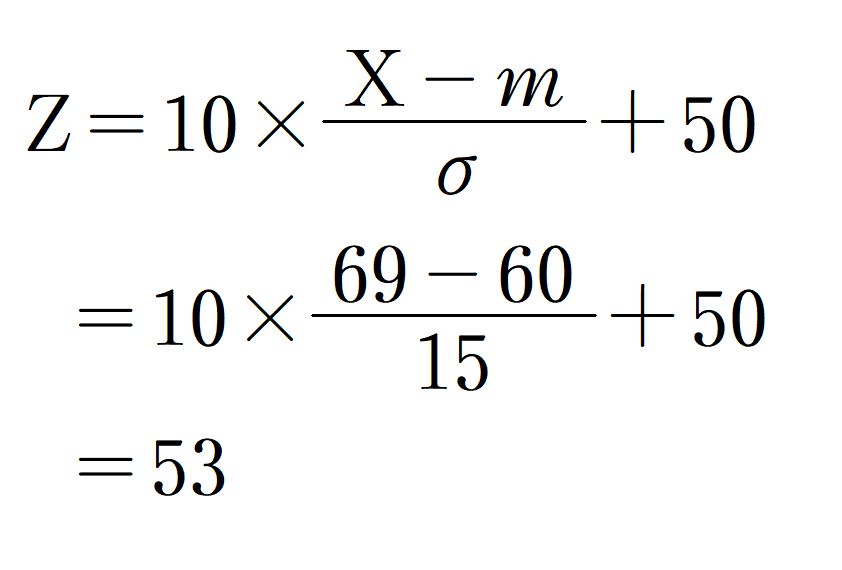
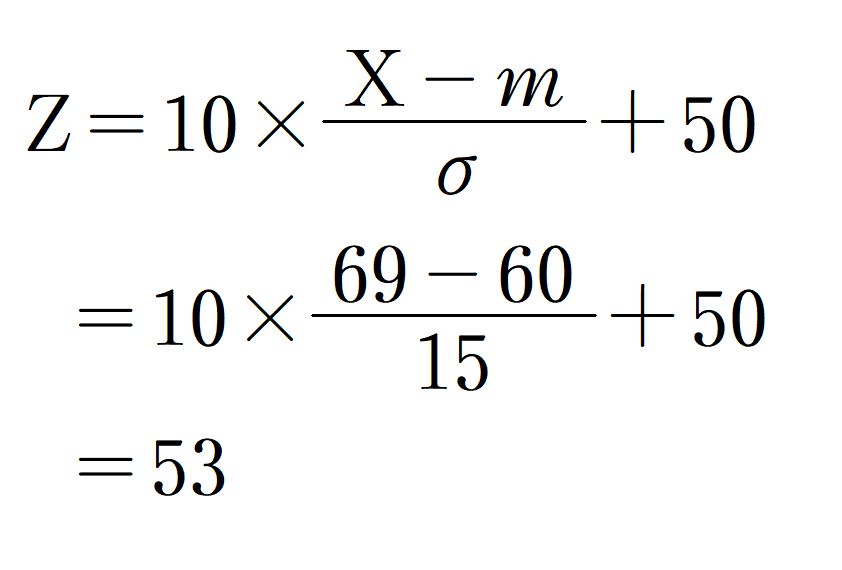
となることがわかります。
達成目標偏差値から、試験で何点取れればよいかを計算する
大学入試を目指す際に、お子さま本人は、志望校の入試で合格できる偏差値は当然知っているはずです。
その前段階での模擬試験において、その偏差値を達成できるかを試していくことでしょう。
そこで、必要な偏差値から、模擬試験で取るべき点数を割り出す方法を説明します。
先日行われた模擬試験の結果は次のとおりでした。
- 平均点は52点
- お子さまの点数は61点で、偏差値は55でした
- お子さまの志望校の偏差値は62です
では、お子さまは次の模擬試験(難易度は変化しないものとする)で何点を目標にすればよいでしょう?
模擬試験が行われた後、成績表がもらえるのですが、その中で、試験の標準偏差は普通書かれないことが多いと思われます。なぜなら、一般の人は標準偏差の値を解釈しないからです(数値の利用法も普通は知りませんし)。ですから、模擬試験の成績表から読み解こうとすれば、上記のように平均点・お子さまの得点と偏差値くらいしかわからないのです。これが実情です。
このケースの場合、次のように計算をします。
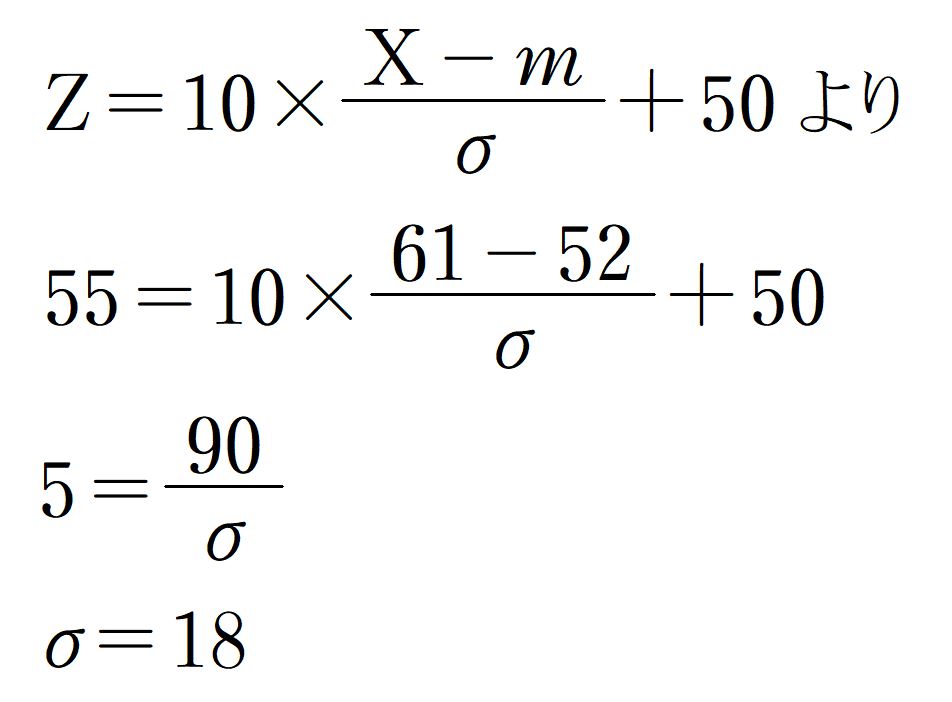
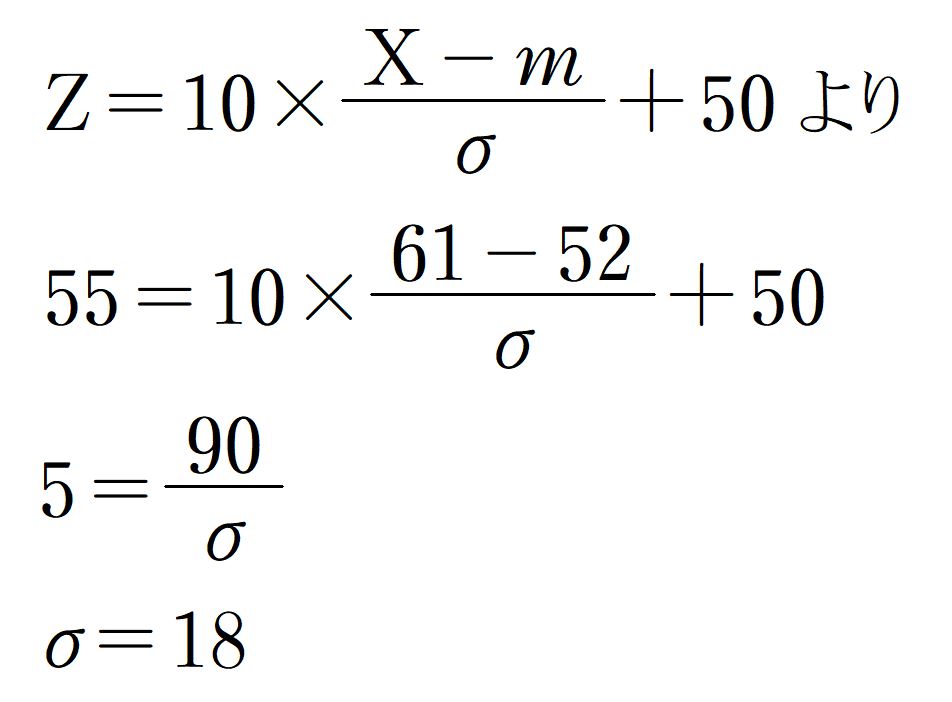
要は先日行われた模擬試験で、大学の目標偏差値の学力を有する人であれば何点取れたのかを計算する方法です。
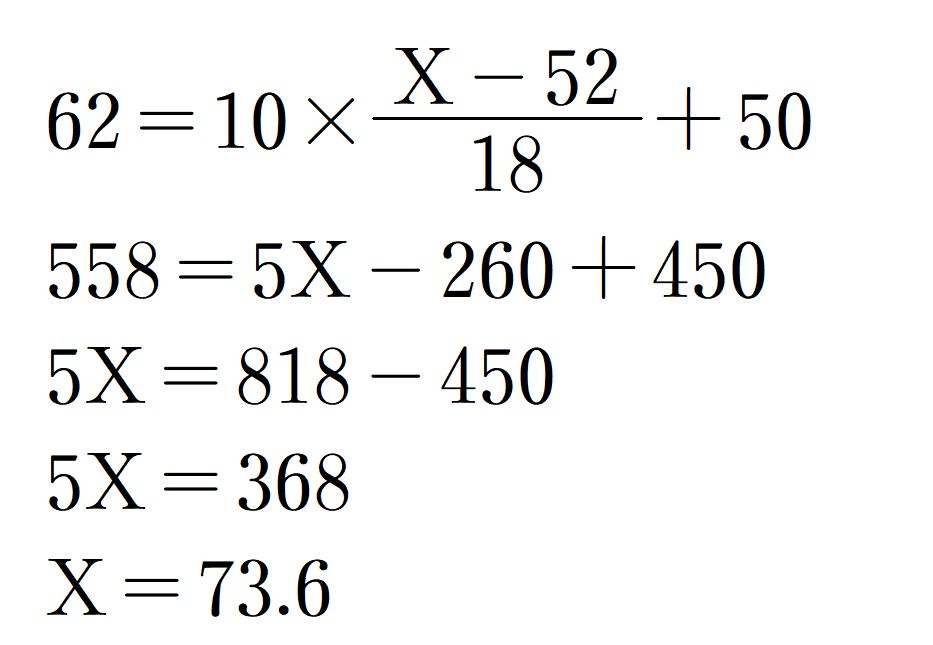
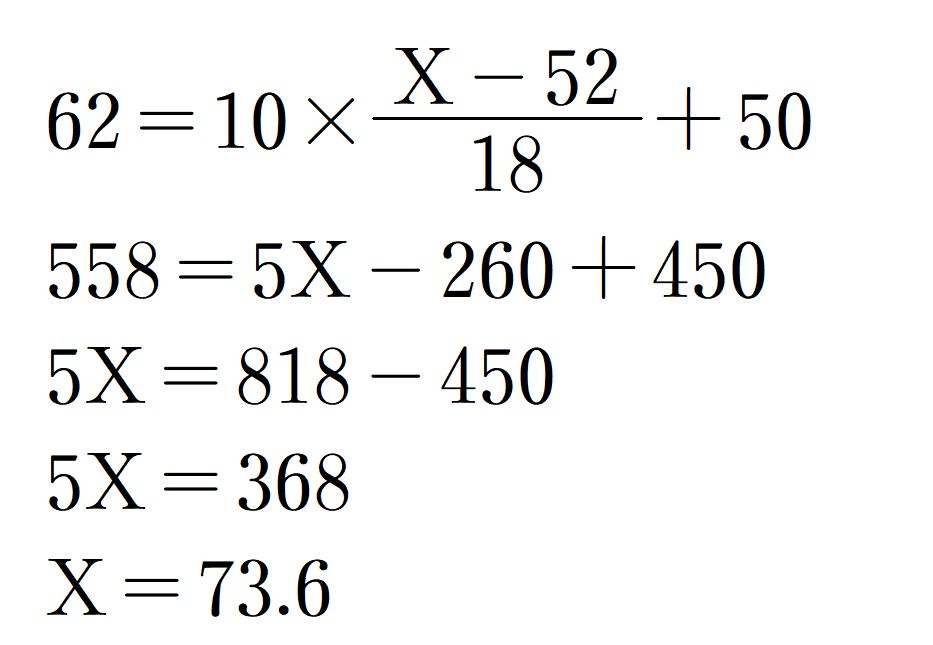
ということで、74点を取れるようになればよいということで、次回の模擬試験ではこれ相当の成績を目標にすると良いです。

このように偏差値をうまく利用すれば、具体的な学習の計画を立てられます。
まとめ
模擬試験は何かと準備がやりにくいところがありますが、偏差値の観点から、「◯点を取るために、この単元をしっかり理解してここまで解けるようにする」といった細かな目標が立つでしょう。実際模擬試験前には学校から過去問のプリントが配られ、それを解いてみるという準備が大多数で、そこから進んで自分流の学習に落とし込めている人はごくわずかではないかと感じます。



模擬試験の結果をどうその後の学習に反映させるかという方法についてはまたいつか記事を書く予定です。
偏差値についての認識が新たになった方や、偏差値の扱い方や学力の把握のしかた、また計画の立て方がわかったという方がおられれば幸いです。
また、このような方法もあるのではないか?という発見があった方、コメントなどをくださると嬉しいです。

コメント